1. 逻辑只有“真”和“假”两值，有“非”单目运算和“与”、“或”、“异或”双目运算。下面运算正确的是：

A.  非“真”＝“假”

B.  非“假”＝“真”

C.  “真“与“真”＝“真”

D.  “真“与“假”＝“假”

E.  “假“与“真”＝“假”

F.  “假“与“假”＝“假”

G.  “真“或“真”＝“真”

H.  “真“或“假”＝“真”

I.  “假“或“真”＝“真”

J.  “假“或“假”＝“假”

K.  “真“异或“真”＝“假”

L.  “真“异或“假”＝“真”

M.  “假“异或“真”＝“真”

N.  “假“异或“假”＝“假”

2. 甲、乙、丙、丁四人要派出两人执行一项任务，如果甲不去，乙就要去；如果乙不去丙就要去；如果丙不去丁就要去，如果丁不去甲就要；甲被派去了，另外一个人是谁？

3. 甲、乙、丙、丁四人要派出两人执行一项任务，如果甲去乙就一定要去；如果乙去丙就一定要去；丁被派去了，另外一个人是谁？

4. 甲、乙、丙、丁四人要派出两人执行一项任务，甲和乙至少要去一个；乙和丙至少去一个；丙和丁也至少要去一个；丁被派去了，另外一个人是谁？

5. 甲、乙、丙、丁四人要派出两人执行一项任务，如果甲和乙只有一个人去则丙一定要去；乙和丙只有一个人去则丁一定要去；丁没有被派去，谁被派去？

6. A、B、C、D四人共有2个球，每人最多1个球，A和B、B和C、C和D、D和A都不能同时有球，一个球在A手上，另一个球在谁手上？

7. A、B、C三个人只一个球，三人都说自己没有，C还说A和B都说假话，说真话的人都说真话，说假话的人都说假话，问球在谁手上？

8. 已知“路程＝速度×时间”。甲乙两地相距500千米，汽车以每小时25千米的速度从甲地到乙地，需要多少小时？

9. 已知“段数＝距离÷段距  两端点都不含中间点数＝段数－1”。甲乙两地相距100千米，公路两边都植一排树，树距5米，始点与终点都不种，问需要种多少棵树？

10. 已知“多脚物头数＝(总脚数－总头数×每个少脚物脚数)÷(每个多脚物脚数－每个少脚物脚数)  如有多头可用分数化为单头”。3头7尾的怪鸟与5头9尾怪物在一起，共有头118个，脚230个，问怪鸟和怪物各有多少个？

11. 下列各组数的最后一个数都丢失了，按规律把它补回：

A.  2, 4, 6, 8, 

B.  2, 4, 8,16,

C.  1, 1, 2, 3, 5, 8,

D.  2, 6, 12, 20, 30,

12. 下面最后一组对象弄丢了，按规律补上：

A.  1-3-2-4，4-1-3-2，2-4-1-3，

B.  a-d-b-c，c-a-d-b，b-c-a-d，

C.  @#$&，#$&@，$&@#，

D.  励精图治，图励治精，治图精励，

13. 根据现有的情况猜想：

A.  2÷2＝1, 4÷2＝2, 6÷2＝3

B.  123÷3＝41, 546÷3＝182, 798÷3＝266

C.  4＝2×2, 6＝2×3, 8＝2×2×2, 10＝2×5

D.  

0.1……＝1/9

0.2……＝2/9

0.3……＝3/9

0.4……＝4/9

0.5……＝5/9

0.6……＝6/9

0.7……＝7/9

0.8……＝8/9

14. 甲乙两地相距60千米，小明从甲地出发往乙地，速度每小时10千米，出发1小时后，由于有突发情况要提前1小时到达。问小明要要怎么办？

15. 找出下面变化中，什么是不变的：

A. 小明12岁，小明爸爸42岁，过来几年，他们的年龄都变大了。

B. 小明身高150厘米，小明爸爸身高175厘米，站在一起拍照，照片中，他们的身高都变小了。

C. 汽车匀速行驶，2小时后走了120千米，又过来一些时间，走的路程变大了。

D. 甲汽车每小时50千米，乙汽车每小时60千米，两小时后，甲汽车走了100千米，乙汽车走了120千米，又过了些时间，甲、乙汽车走的路程都变化了。

E. 小明从甲地到乙地，用了5小时，回来时，速度提高了，时间缩短了。

16. 下面说法正确的是：

A. 在集合中至少有一个元素符合条件，称作“有可能”。

B. 如果集合中所有元素都符合条件，称“一定是”。

C. 如果集合中所有元素都不符合条件，称“不可能”。

D. 可能性可以用≧0与≦1的数来表示，这个数称“概率”。

E. “有可能”的概率范围是＞0和≦1。

F. “不可能”的概率＝0。

G. “一定是”的概率＝1。

17. 在一个盒子中有红绿蓝三个球体，另一个盒子中红绿蓝三个正方体，从两个盒子中分别抽出一个物体，问抽到红球和红正方体的可能性(概率)是多少？

18. 盒子中有80个红球、18个绿球和5个蓝球，问至少要拿多少个球才能保证有10个红球？

19. 有两变量，a＝34，b＝75，不引用第三个变量，好像无法进行数值调换，因为如果赋值a＝b，那a原来的值就丢失。事实上是可以的，你能想出是什么方法吗？

附录1

小学数学心法之十三——逻辑与可能性

只两值，真与假，或与非，异或算。

或运算，一值真，它不看，也是真。

与运算，一值假，它不看，也是假。

非运算，真变假，假变真，非非原。

异或算，两个值，不相同，才为真。

不是真，即是假，反之同，排中律。

逻辑题，先列表，逻辑算，排中律。

狗会死，它是狗，它会死，三段论。

类为真，属此类，亦为真，演绎法。

看题目，先分类，用演绎，解问题。

时距速，有公式，路程题，套公式。

打标点，植树题，知间距，明头尾。

鸡与兔，鸭与猪，虽有异，解法同。

林中鸟，个个飞，鸟会飞，归纳法。

集合中，个个真，此集合，就是真。

找规律，归纳法，从个别，到一般。

所有鸟，未目睹，应会飞，猜想法。

此猜想，未必真，看鸵鸟，只会跑。

然猜想，尤重要，提问题，树创新。

二四六，二除尽，可猜想，二尽偶。

一二三，三除尽，三连数，三除尽。

九除一，一循环，九除二，二循环。

九除八，八循环，九除九，九循环。

数关系，多因果，怎样解，因果法。

哪是因，哪是果，图与表，莫轻略。

因果数，多乘除，乘或除，要分清。

千变化，万变化，解问题，不变法。

自龄增，亲龄增，年龄差，不变化。

照片中，都变矮，身高比，不变化。

匀速走，时间增，路程增，比不变。

速不同，路程比，时虽变，比不变。

集合中，至少一，判为真，有可能。

这情况，如全真，称之为，一定是。

集合中，找不到，一个真，不可能。

可能性，有大小，零至一，来标定。

不可能，数是零，一定是，数是一。

有可能，分数值，取数值，同分数。

附录2  “第十二章 数据”详解

1. 下面有关平均值的说法正确的是：

A. 平均值一定会出现在求平均值的那组数中。 错误

B. 一组数的一个最小值加一个最大值的和除以2就是这组数的平均值。 错误

C. 一组数的每一个数减这组数的平均值，所有差之和等于0。 正确

D. 一组数的平均值减每一个数，所有差之和等于0。 正确

E. 平均值可以用来比较两组数的大小。 正确

说明：平均即是取长补短，平均值等于总和除以个数。平均值不一定出现在这组数中；也不一定等于头尾相加除以二；平均值与每个数的差有正有负，这些差之和必为0；平均值是比较两组数据大小的重要指标。

2. 下面有关统计图的说法正确的是：

A. 分析数值的趋势用条形统计图。 错误

B. 对比数值之间的差异用折线统计图。 错误

C. 分析各部分数值在总值中的占比用扇形统计图。 正确

说明：在非指定的情况下，用条形统计图对比数据项的差别；用折线统计图分析数据趋势；用扇形统计图分析部分的占比。

3. 小明五次数学考试成绩如下：

第一次  71

第二次  80

第三次  87

第四次  92

第五次  95

用适当的统计图分析数据并作出总结。

解：因为同一对象的不同时间的数据，一般需要分析趋势，所以用折线统计图：

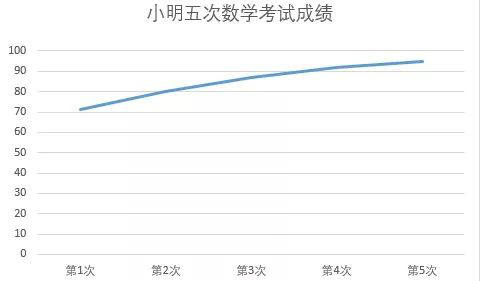
总结：小明的数学成绩在不断提高，90分前提高较快，90分后提高较慢。

手工作图：折线统计图的折线所在的横坐标范围应该不小于三分之二；纵坐标长度一般不超过横坐标，原点值一般是0，不过如果数值较大原点也可以取一个比最小值小的整数，使折线纵坐标范围在三分之二左右。

4. 小王的期末考试各科成绩如下：

语文  96

英语  95

数学  76

用适当的统计图分析，并总结小王的各科乘积的状况。

解：因为同一集合(小明的考试成绩)的不同对象在同一时间的数据，一般需要对比，所以用条形统计图：

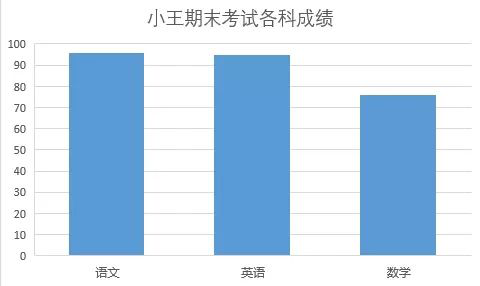
总结：小王的语文和英语成绩比较好，数学成绩较差。

手工作图：条形统计图的纵坐标长度一般不超过横坐标，原点值一般是0，不过如果数值较大，原点也可以取一个比最小值小的整数，使条形易于观看和对比。

5.  五班共50 (改60)人，一次数学考试，各分数(无小数)段人数如下：

90分以上：15

80分到89分：25

70分到79分：10

60分到69分：8

59分以下：2

用适当的统计图分析这次数学考试成绩，并作出总结。

解：因为同一整体(五班)的不同部分在同一时间的数据，一般需要分析占比，所以用扇形统计图。

15+25+10+8+2＝60

360÷60＝6

15×6＝90

25×6＝150

10×6＝60

8×6＝48

2×6=12

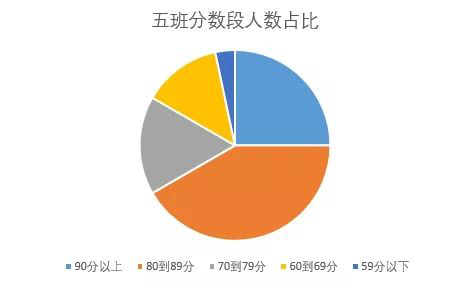
总结：80到89分人数最多，其次是90分以上和70到79分，再其次是60到69分，59分以下人数最少。

手工作图：直接算出角度。

备注：本文为了省时间，用了电子表格制图。

​